Cuando comencé a utilizar la analítica de datos, hace unos 15 años, ni siquiera era consciente de estar haciendo algo especialmente relevante. Ahora forma parte de mi modo de trabajar.
Supongo que como docentes os tocará enfrentaros cada trimestre a como quiera que lo llaméis en cada lugar: la tabla, el cuadrante, la planilla, la sábana, el pliego,… en definitiva, un sinfín de números ordenados en filas y columnas, habitualmente impresos en blanco y negro, y de vez en cuando con elementos de formato que destacan las notas inferiores a 5 con negrita, cursiva, subrayado, sombreado, o combinaciones varias de los anteriores.
El primer año que fui tutor, me encontré con una de esas hojas con 30 filas y 12 columnas de datos. Algo como esto, dividido en tres hojas:
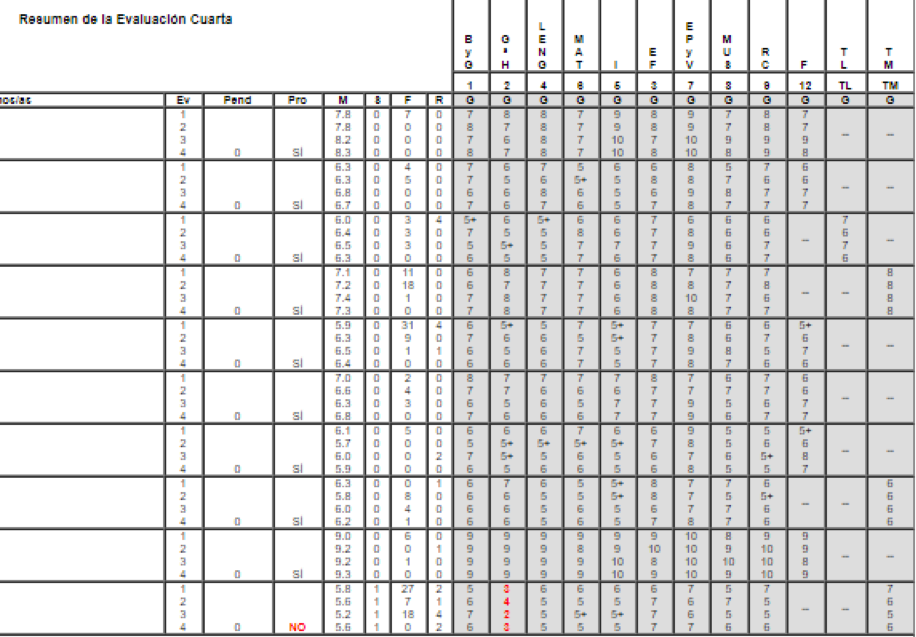
Necesitaba encontrar una manera de obtener información relevante de todos esos datos, y estaba claro que debía ser algo visual.
Lo primero que tenemos que tener claro antes de lanzarnos a hacer gráficos es el propósito. ¿Qué necesito saber? ¿Qué información es relevante? Y a partir de ahí empezamos a trabajar.
Para analizar los resultados de la clase al final de una evaluación, quiero saber:
- Cómo han sido globalmente los resultados (distribución de notas)
- Cuántos alumnos tienen dificultades (distribución del número de suspensos)
- En qué alumnos se concentran los mejores y los peores resultados (esto normalmente ya lo sabemos antes de analizarlo, pero a veces hay sorpresas)
- En qué materias hay discordancias con respecto al promedio
¿Cómo obtengo cada uno de esos inputs?
1 Distribución de notas
Utilizo la función =CONTAR.SI($intervalo$;nota) para saber la frecuencia de cada nota global, realizo una tabla y sobre ella y dibujo la gráfica.
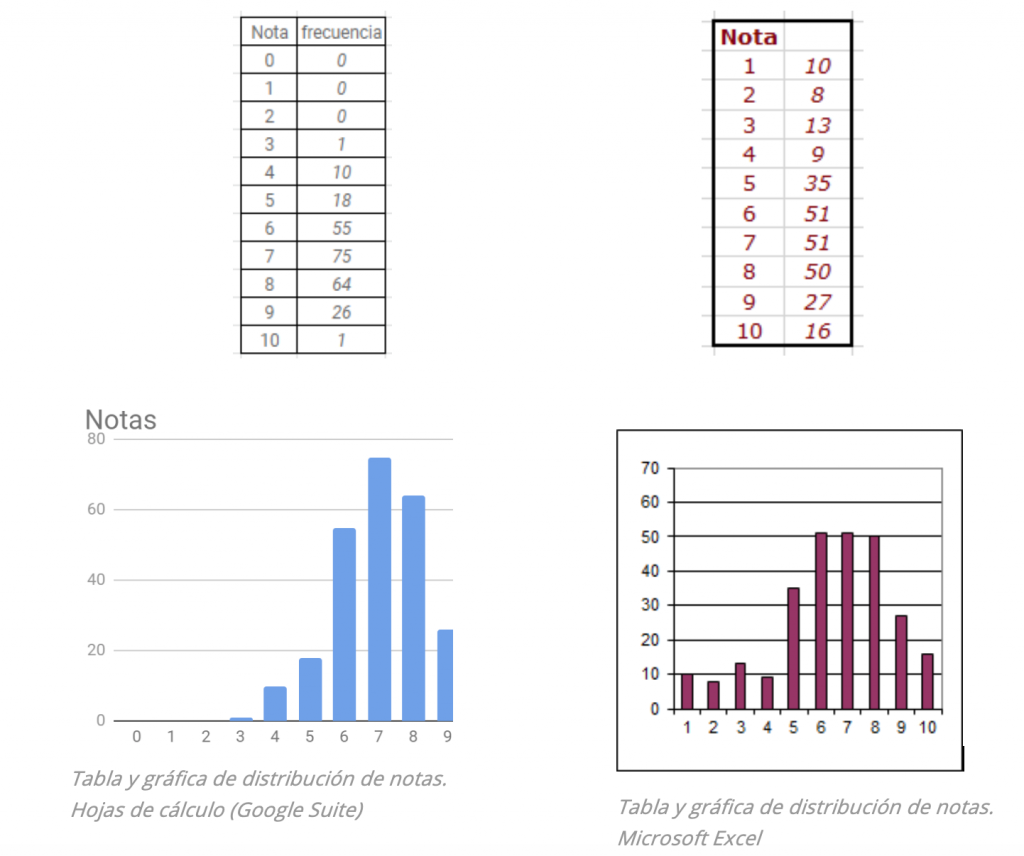
Podemos ver de manera mucho más clara y rápida cómo es globalmente cada una de las clases.
La primera, apenas presenta alumnos con calificaciones bajas, y la mayoría de puntuaciones se concentran alrededor del 7. La frecuencia de la nota 10 es mínima.
En la segunda clase hay mucha más diversidad. Mayor número de alumnos con calificaciones bajar, pero a su vez también hay mayor frecuencia de los valores 9 y 10.
A partir de esta información, el docente tiene que ser capaz de diseñar estrategias específicas para cada una de las dos clases, lo mismo no funcionará de la misma manera.
2 Alumnos con dificultades
El número de suspensos total en una evaluación da una información parcial, ya que ante un número elevado podría tratarse de pocos alumnos que concentran muy malos resultados o bien muchos alumnos con pocos suspensos cada uno de ellos. Utilizo la función CONTAR.SI(intervalo; “<5”) para calcular el número de suspensos de cada alumno (muchas veces lo hace ya el programa de notas que utilizamos), y elaboro una nueva tabla. De nuevo, con CONTAR.SI(intervalo;número) para establecer cuántos alumnos tienen un número de suspensos determinado.

En ambas clases hay un número total de suspensos igual, pero se distribuyen de manera diferente. En la primera clase vemos cómo la mayoría de alumnos no presentan dificultades en ninguna materia, concentrando todos los suspensos un número reducido de alumnos, mientras que en el segundo ejemplo, son minoría los alumnos con todas las asignaturas aprobadas, y los suspensos se reparten de manera más homogénea.
Si nos fijamos en los alumnos que tienen entre 1 y 3 suspensos, en el primer ejemplo representan una minoría, pero son mayoría en la segunda clase de muestra.
3 Mapa de color
El mapa de color nos servirá para indentificar en qué alumnos o en qué materias se concentran los mejores y los peores resultados de la clase.
La manera de elaborar el mapa de color es tan sencilla como escoger un formato condicional, que asigne diferentes colores a las notas que figuran en la tabla. Para este formato, podremos elegir la escala de colores que queramos, pero en el ejemplo seguiré el tradicional código de colores rojo (dificultad) – amarillo – verde.
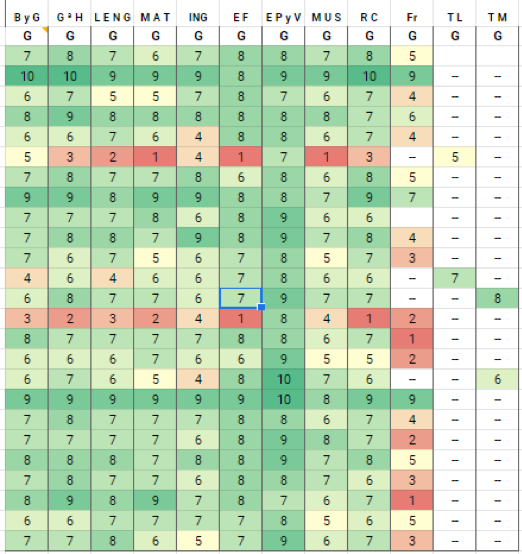
En un solo golpe de vista podemos identificar a dos alumnos que tienen dificultades en muchas materias (filas con predominio rojo), a otros dos que obtienen muy buenos resultados (filas verdes más intensas).
Del mismo modo, si nos fijamos en las columnas, podemos observar que en una de ellas todos los alumnos obtienen puntuaciones altas mientras que en otra el número de suspensos es elevado.
4 Situación de materias con respecto al promedio
En el apartado anterior hemos visto cómo se pueden identificar situaciones anómalas que son llamativas por existir una concentración de valores extremos, tanto por arriba como por abajo.
Sin embargo, cuando la distribución de notas es más desigual nos costaría visualizar en qué materias se están consiguiendo resultados por encima o por debajo del promedio. Para calcularlo, bastaría con añadir una línea en nuestra tabla de notas y calcular la función PROMEDIO(intervalo). Complementariamente, una vez realizado este cálculo del promedio, podemos insertar una gráfica en la que se muestren estos resultados y el promedio global de todas las asignaturas.
Así, podremos visualizar fácilmente las asignaturas en las que se están obteniendo resultados inferiores o superiores.
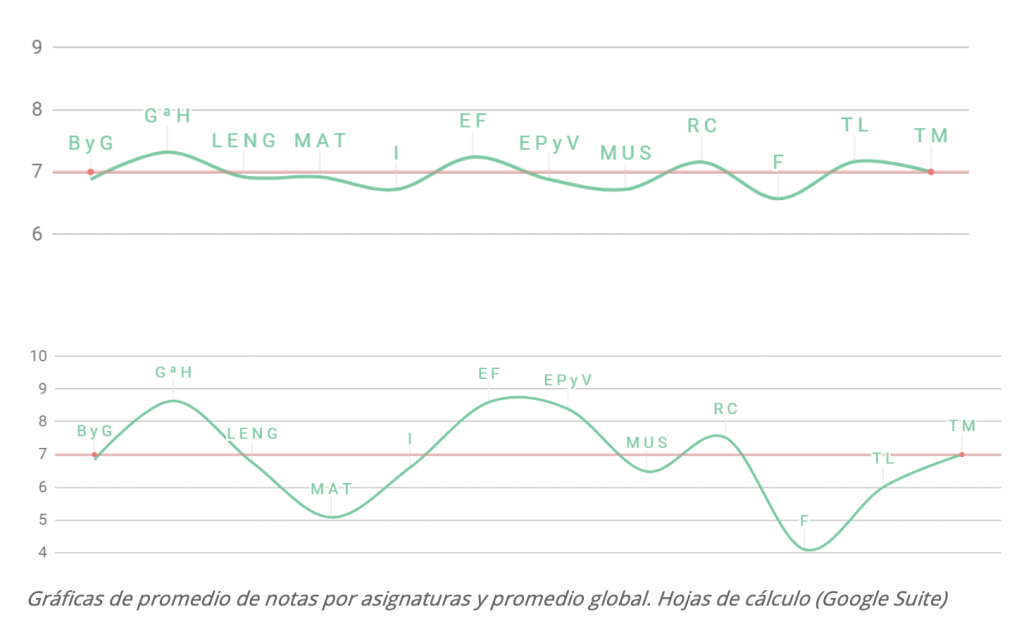
En ambas clases, el promedio global es un 7, pero la distribución de notas en cada asignatura es diferente.
En el primer ejemplo, los resultados son más homogéneos, sin grandes disparidades entre unas materias y otras. Ninguna nota promedio baja del 6,5 ni sube del 7,5. Sin embargo, la segunda muestra arroja resultados que oscilan entre el 4 y el 9.
El análisis de todos estos resultados nos lleva a identificar distintas realidades dentro del aula, lo que nos permitirá tomar decisiones y establecer líneas de actuación específicas. Si no lo hacemos, habremos presentado a nuestro claustro unos resultados muy bonitos, haremos una reflexión descriptiva, pero no habrá servido para el principal objetivo, que es mejorar nuestros procesos de enseñanza-aprendizaje.